2022년 4월 15일 - BST, AVL 트리

1. BST

- 특징

BST는 Binary Search Tree (이진 탐색 트리)의 준말.

 

BST는 이진 트리이면서, 아래와 같은 성질을 가지고 있다.

•각 노드에 값이 있다.

•값들은 전순서가 있다.

•노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.

•노드의 오른쪽 서브트리에는 그 노드의 값보다 큰 값들을 지닌 노드들로 이루어져 있다.

•좌우 하위 트리는 각각이 다시 이진 탐색 트리여야 한다.

•중복된 키를 허용하지 않습니다.

 

- 삽입 알고리즘

1. 새로운 노드를 생성하고, 만약 BST가 비어있다면 root에 새로운 노드를 할당합니다.

2. 만약 BST가 비어있지 않다면 내부함수 _insert를 호출합니다.

3. _insert에서 root가 비어있다면 새로운 함수를 반환합니다.

4. 그리고 root가 비어있지 않다면 root와 새로운 노드의 값을 비교해서 _insert 함수를 재귀호출합니다.

- 삭제 알고리즘

1. 삭제하는 노드에 자식 노드가 없는 경우

2. 삭제하는 노드에 오른쪽 자식 노드만 존재하는 경우

3. 삭제하는 노드에 왼쪽 자식 노드만 존재하는 경우

4. 삭제하는 노드에 왼쪽과 오른쪽 자식 노드가 모두 존재하는 경우

 

 

1번의 경우에는 삭제하는 노드가 leaf 노드이며, 단순히 삭제만 하면 됩니다. 2번과 3번의 경우에는 삭제할 노드 위치에 자식 노드를 연결해주고, 삭제하면 됩니다. 4번의 경우에는 두 가지의 방법이 존재하는데, 1)왼쪽 서브트리에서 가장 큰 노드를 삭제할 노드 위치로 옮기거나, 2)오른쪽 서브트리에서 가장 작은 노드를 삭제할 노드 위치로 옮기고, 삭제를 진행하면 됩니다.

- 검색 알고리즘

•이진탐색트리에서 키 x를 가진 노드를 검색하고자 할때, 트리에 해당 노드가 존재하면 해당 노드를 리턴하고, 존재하지 않으면 NULL을 리턴한다.

•검색하고자 하는 값을 루트노드와 먼저 비교하고, 일치할 경우 루트노드를 리턴한다.

•불일치하고 검색하고자 하는 값이 루트노드의 값보다 작을 경우 왼쪽 서브트리에서 재귀적으로 검색한다.

•불일치하고 검색하고자 하는 값이 루트노드의 값과 같거나 큰 경우 오른쪽 서브트리에서 재귀적으로 검색한다.

 

2. AVL 트리

- 특징

AVL 트리에서 AVL은 발명자의 이름인 Adelson-Velsky and Landis 에서 따온 이름이다. AVL 트리는 엄격하게 균형을 유지하기 때문에 Red-black 트리보다 더 빠른 성능을 가지지만 더 많은 작업을 수행해야만 한다.

AVL 트리는 다음과 같은 성질을 가진다.

•AVL 트리는 이진 탐색 트리의 속성을 가집니다.

•왼쪽, 오른쪽 서브 트리의 높이 차이가 최대 1 입니다.

•어떤 시점에서 높이 차이가 1보다 커지면 회전(rotation)을 통해 균형을 잡아 높이 차이를 줄입니다.

•AVL 트리는 높이를 logN으로 유지하기 때문에 삽입, 검색, 삭제의 시간 복잡도는 O(logN) 입니다.

BF = hL(왼쪽 서브트리의 높이) – hR(오른쪽 서브트리의 높이)

BF값이 -1, 0, 1 일 때 균형있는 트리이다.

각 노드에 대한 BF 값을 계산하여 값이 -1, 0, 1이 아닐 경우 불균형 트리이므로 균형을 맞추기 위해 회전 기법을 사용한다. 삽입 삭제는 BST와 동일하나 삭제과정에서 불균형을 확인하는 과정이 추가되었다.

 

- 회전 기법

1) LL유형 => 우회전

2) RR유형 => 좌회전

3) RL유형 => 두번째 노드를 좌회전한 후, 전체 노드 우회전

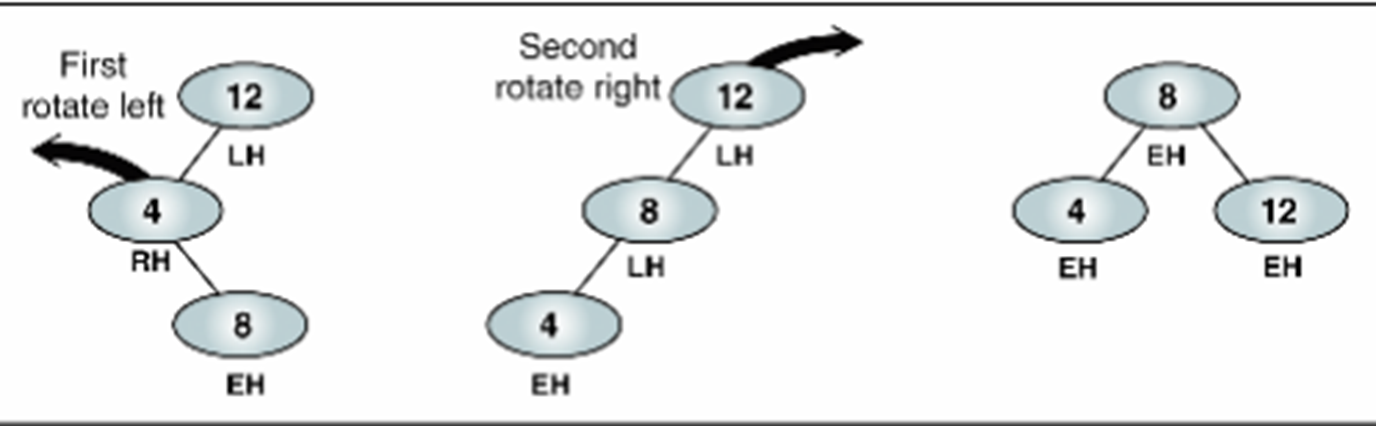
4) LR유형 => 두번째 노드를 우회전한 후 전체 노드 좌회전

 

3. 출처

[출처]

https://junstar92.tistory.com/67 [BST]

https://yoongrammer.tistory.com/71 [BST]

https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=dhdh6190&logNo=221062784111 [AVL]

https://walbatrossw.github.io/data-structure/2018/10/26/ds-avl-tree.html [AVL]