고정 헤더 영역
상세 컨텐츠
본문
난이도 1인데 푸는데 오래 걸리고 관련 자료도 많이 찾아봤다... 난이도 1인데도 어렵다...^_^...
문제는 아래와 같다.

위의 문제에 대한 나의 문제 풀이는 아래와 같다.
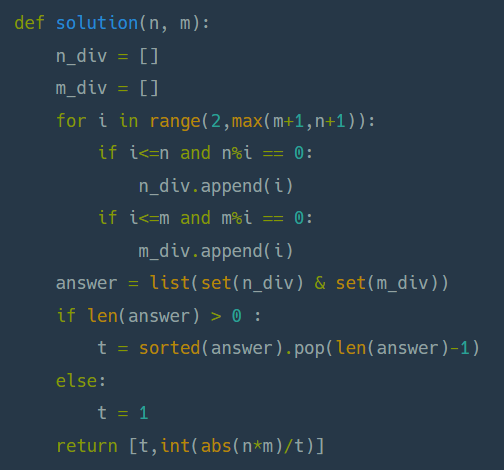
나의 문제 풀이 해석을 진행한 후 다른 문제 풀이 방식도 해석해보겠다.
n_div와 m_div를 선언하여 n과 m 각각의 약수들을 삽입한다. 이 때 1과 자기자신의 수는 제외한 나머지 약수들을 삽입한다. 그리고 두 리스트를 set으로 변환하여 and 연산한다. 그 결과가 존재한다면 리스트를 정렬하고 가장 끝의 원소를 최대공약수로 반환한다. 만약 결과가 존재하지 않는다면 중복되는 약수가 존재하지 않음으로 최대공약수는 1을 반환한다. 함수는 최대공약수와 함께 최소공배수도 반환해야 하므로 최대공약수를 이용하여 최대공배수를 구하는 공식인 두 수의 곱의 절댓값을 최대공약수로 나누는 방식으로 최대공배수도 동시에 반환한다.
위의 문제풀이에서 최대공약수를 이용하여 최소공배수를 구하는 방법은 검색을 통해 풀이했다. 정말 코딩 테스트에서는 수학 공식을 알면 쉽게 풀 수 있는 문제들이 자주 나오는 것 같다.
나의 코드와 비교할 코드를 살펴보자.

코드 해석을 해보면, a b 중 크고 작은 값을 지정해주기 위해 max 함수와 min 함수를 이용하여 큰 값을 c로 작은 값을 d로 지정했다. 그리고 변수 t 에 1을 저장했다. while 반복문을 사용하여 t가 0보다 클 경우를 조건으로 선언했다. 만약, t가 0보다 클 경우 t는 c를 d로 나눈 나머지 값이 되고 c, d는 d, t가 된다.
이 부분이 어떻게 동작하는지 이해하기 위해서는 유클리드 호제법에 대해 알아야 한다. 위키백과에서는 유클리드 호제법에 대해 다음과 같이 설명한다.
| 유클리드 호제법(-互除法, Euclidean algorithm) 또는 유클리드 알고리즘은 2개의 자연수 또는 정식(整式)의 최대공약수를 구하는 알고리즘의 하나이다. 호제법이란 말은 두 수가 서로(互) 상대방 수를 나누어(除)서 결국 원하는 수를 얻는 알고리즘을 나타낸다. 2개의 자연수(또는 정식) a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다. 이 성질에 따라, b를 r로 나눈 나머지 r'를 구하고, 다시 r을 r'로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수이다. 이는 명시적으로 기술된 가장 오래된 알고리즘으로서도 알려져 있으며, 기원전 300년경에 쓰인 《원론》 제7권, 명제 1부터 3까지에 해당한다. |
간단히 말하면 유클리드가 발견한 최대공약수를 구하는 알고리즘이다. 이를 이용하는 방법은 위의 비교할 코드의 반복문 내의 식과 동일하다. 이와 관련된 위키백과의 예시를 하단에 첨부하겠다.

앞으로 최대공약수 최소공배수 문제가 나온다면 꼭 유클리드 호제법을 이용하여 풀도록 하자.
'컴퓨터 공부 > 알고리즘' 카테고리의 다른 글
| [프로그래머스] 예상 대진표 (0) | 2021.12.30 |
|---|---|
| [프로그래머스] 다단계 칫솔 (0) | 2021.12.30 |
| [프로그래머스] 자연수 뒤집어 배열로 만들기 (0) | 2021.12.28 |
| [프로그래머스] 행렬의 덧셈 (0) | 2021.12.25 |
| [프로그래머스] 소수 만들기 (0) | 2021.12.23 |





댓글 영역