고정 헤더 영역
상세 컨텐츠
본문
2021년 12월 23일 프로그래머스에서 약수의 개수와 덧셈 풀이라는 문제를 풀었다.
나는 문제풀이 코드는 다음과 같다.

그러나, 저렇게 풀면 중첩 반복문으로 인해서 코드의 시간복잡도가 엄청 올라간다. 시간 복잡도는 O(n^2) 로 예상된다.
위의 방식으로 풀고 난 후, 프로그래머스의 기능인 다른 사람의 풀이를 통해 다른 사람들의 코드를 살펴보았다. 그 중 사람들이 제일 많은 댓글을 남긴 다음의 코드를 소개하고 분석하고자 한다.

시간이 얼마나 차이나는지 확인하기 위해 프로그래머스에서 측정 시간을 비교해 보았다.
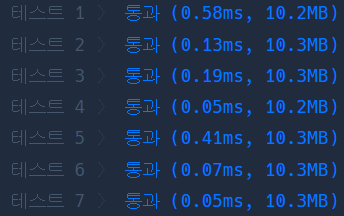

왼쪽은 너무나도 아름다운데에 반해 오른쪽은... 당장이라도 코딩테스트 1번 문제 광탈할 상이다.
그러므로 해당 코드는 어떻게 문제를 풀었고, 왜 속도가 빠른지 낱낱히 비교 분석해보도록 한다. 분석하기 전, 문제에 대해 다시한번 짚고 가겠다.

따라서 문제를 풀기 위해선 약수를 구해야 하고, 약수의 개수를 세야 한다. 따라서 본인은 약수 문제풀이의 기본 방식인 n % i == 0 의 방법을 이용하여 문제를 풀었다. 하지만 이 방법은 각 수 하나당 1 ~ n 까지의 반복문을 매번 실행해야 한다. 따라서 시간이 n ^ 2 으로 증가한다.
이제 아름다운 코드를 살펴보자.
처음으로 눈에 띄는 부분은 ** 산술 연산자다. 이 연산자는 제곱을 나타내는 연산자인데 if 문에서 i 를 0.5 제곱한 값의 int 값과 i ** 0.5 한 값을 비교하여 같으면 약수의 개수가 홀수인 것으로, 다르면 약수의 개수가 짝수인 것으로 판별했다. 이를 이해하기 위해 해당 코드를 pycharm에서 디버깅 해보겠다.
i가 13인 경우 좌측의 값은 3, 우측의 값은 3.60555... 로 일치하지 않아 약수의 개수가 홀수라고 판별했다.

어떻게 위의 방법으로 푸는 것이 가능한 것일까?
해당 문제 풀이 방식의 "제곱수(자연수를 2번 곱해서 나오는 정수)의 약수의 갯수는 항상 홀수이다." 댓글에서 힌트를 찾을 수 있었다.
제곱수는 약수의 갯수를 항상 홀수로 지니고 있는 성질을 가지고 있으므로 제곱수인 경우에는 약수의 개수가 홀수이고, 제곱수가 아닌 경우는 짝수라고 판단할 수 있다.
if int(i**0.5)==i**0.5따라서 위의 if문은 i의 제곱근이 자연수인지 아닌지를 파악하여 'i의 제곱근이 자연수이면 제곱수이고 i의 제곱근이 자연수가 아닌 경우는 제곱수가 아니다.' 를 이용한 문제 풀이 방식이다.
다음에 약수 관련 문제 풀이시에 반드시 기억해야 겠다.
결론
제곱수는 약수의 개수가 홀수 이다. 즉, x의 제곱근이 자연수이면 (= 제곱수)이면 약수의 개수가 홀수 이다.
'컴퓨터 공부 > 알고리즘' 카테고리의 다른 글
| [프로그래머스] 다단계 칫솔 (0) | 2021.12.30 |
|---|---|
| [프로그래머스] 최대공약수와 최소공배수 (0) | 2021.12.29 |
| [프로그래머스] 자연수 뒤집어 배열로 만들기 (0) | 2021.12.28 |
| [프로그래머스] 행렬의 덧셈 (0) | 2021.12.25 |
| [프로그래머스] 소수 만들기 (0) | 2021.12.23 |





댓글 영역